Interpolasi Tropis
Frank Sottile
9 Oktober 2004, College Station, Texas.
Semua orang tahu bahwa dua titik menentukan garis, dan banyak orang yang telah mempelajari geometri tahu bahwa lima poin di pesawat menentukan kerucut. Secara umum, jika Anda memiliki m poin acak dalam pesawat dan Anda ingin lulus kurva rasional gelar d melalui semua dari mereka, mungkin tidak ada solusi untuk masalah interpolasi ini (jika m terlalu besar), atau jumlah tak terbatas solusi (jika m terlalu kecil), atau jumlah terbatas solusi (jika m tepat). Ternyata `` m tepat '' berarti m = 3 d -1 ( m = 2 untuk baris dan m = 5 untuk conics).
Sebuah pertanyaan sulit adalah, jika m = 3 d -1, berapa banyak yang rasional kurva derajat d interpolasi poin? Mari kita sebut nomor ini N d , sehingga N 1 = 1 dan N 2 = 1 karena garis dan kerucut dari ayat sebelumnya yang unik. Telah lama diketahui bahwa N 3 = 12, dan pada tahun 1873 Zeuthen [ Ze ] menunjukkan bahwa N 4 = 620. Itu di mana hal-hal berdiri sampai sekitar sepuluh tahun yang lalu, ketika Kontsevich dan Manin [ KM ] digunakan associativity di cohomology kuantum untuk memberikan rekursi elegan untuk nomor ini.
Tema penelitian di MSRI Musim Dingin 2004 semester Aspek Topological Real Aljabar Geometri termasuk enumerative geometri nyata aljabar, geometri tropis, pesawat belokan nyata, dan aplikasi nyata algebraic geometri. Semua terjalin dalam kisah terungkapnya masalah interpolasi ini, masalah prototipe dari geometri enumerative , yang merupakan seni menghitung angka geometris ditentukan oleh kondisi kejadian yang diberikan. Berikut ini adalah masalah lain: berapa banyak baris dalam ruang memenuhi empat baris yang diberikan? Untuk menjawab ini, diketahui bahwa tiga baris berbaring di hyperboloid ganda diperintah unik.
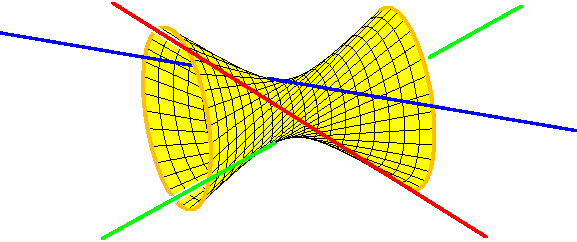
Tiga baris berbaring di salah satu penguasa, dan penguasa kedua terdiri dari garis pertemuan diberikan tiga baris yang. Sejak hyperboloid yang didefinisikan oleh persamaan kuadrat, garis keempat akan bertemu di dua titik. Melalui masing-masing dua titik ada garis dalam putusan kedua, dan ini adalah dua garis bertemu kami empat baris yang diberikan.
Enumerative geometri yang terbaik selama kompleks angka, karena jumlah angka yang sebenarnya tergantung agak halus pada konfigurasi angka memberikan kondisi kejadian.Misalnya, baris keempat dapat memenuhi hyperboloid di dua titik yang nyata, atau di dua titik konjugat kompleks, dan jadi ada dua atau tidak ada garis nyata memenuhi keempat.Berdasarkan banyak contoh, kami telah datang untuk mengharapkan bahwa masalah enumerative mungkin memiliki semua solusi yang nyata [ Jadi ].
Masalah seperti yang lain adalah 12 kurva rasional interpolasi 8 poin dalam pesawat. Kebanyakan ahli matematika yang akrab dengan nodal (rasional) kubik ditampilkan di sebelah kiri bawah. Ada lagi jenis nyata rasional kubik, ditampilkan di sebelah kanan.
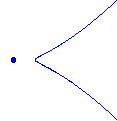
Dalam kurva kedua, dua cabang konjugasi kompleks bertemu di titik yang terisolasi. Jika kita membiarkan N ( t ) menjadi jumlah kurva nyata dari jenis t interpolasi 8 poin yang diberikan, maka Kharlamov dan Degtyarev [ DK ] menunjukkan bahwa
N ( 
) - n ( 
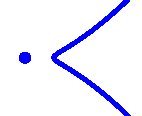) = 8.
Berikut adalah penjelasan dari metode topologi dasar mereka.
Karena ada di paling 12 kurva tersebut, N ( ) + N ( ) \ leq 12, dan jadi ada 8, 10, atau 12 kubik nyata rasional interpolasi 8 poin nyata dalam pesawat, tergantung pada jumlah (0, 1, atau 2) dari cubics dengan titik terisolasi. Dengan demikian akan ada 12 kubik rasional nyata interpolasi setiap 8 dari 9 titik persimpangan dari dua cubics bawah.
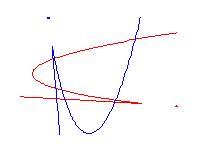
Welschinger [ W ], yang adalah seorang Postdoc MSRI musim dingin lalu, dikembangkan contoh ini menjadi sebuah teori. Secara umum, singularitas dari real rasional pesawat melengkung C adalah node atau titik terisolasi. Paritas jumlah node adalah yang tanda s ( C ), yang 1 atau -1. Mengingat 3 d -1 nyata poin dalam pesawat, Welschinger dianggap nilai absolut dari kuantitas
s ( C ),
jumlah lebih dari semua kurva rasional nyata C derajat d yang interpolasi poin. Dia menunjukkan bahwa jumlah tertimbang ini tidak tergantung pada pilihan poin. Menulis W d untuk invarian ini Welschinger. Sebagai contoh, kita hanya melihat bahwa W 3 = 8.
Ini adalah terobosan, seperti W d adalah (hampir) pertama invarian benar-benar non-sepele dalam enumerative nyata geometri aljabar. Perhatikan bahwa W d adalah batas bawah untuk jumlah kurva rasional riil melalui 3 d -1 nyata poin dalam pesawat, dan W d \ leq N d .
Mikhalkin, yang merupakan penyelenggara semester, disediakan tombol untuk komputasi W d menggunakan geometri aljabar tropis [ Mi ]. Ini adalah geometri dari semiring tropis, di mana operasi max dan + pada bilangan real menggantikan operasi biasa + dan perkalian. Sebuah polinomial tropis adalah fungsi sesepenggal linear dari bentuk
T ( x , y ) = max ( i , j ) { x i + y j + c i , j },
di mana perhitungan adalah dengan operasi aritmatika biasa dan maksimal diambil alih subset terbatas Z 2 dari eksponen T dan c i , j adalah koefisien jumlah riil T . Sebuah polinomial tropisT mendefinisikan kurva tropis, yang merupakan himpunan titik-titik ( x , y ) di mana T ( x , y ) tidak terdiferensiasi. Berikut adalah beberapa kurva tropis.
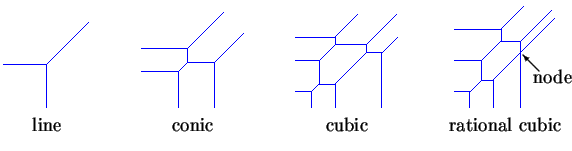
Derajat kurva tropis adalah jumlah sinar cenderung infinity di salah satu dari tiga arah Barat, Selatan, atau Timur Utara. Kurva tropis adalah rasional jika itu adalah perendaman piecewise-linear dari pohon. Node memiliki valensi 4.
Mikhalkin menunjukkan bahwa hanya ada finitely banyak kurva tropis rasional gelar d interpolasi 3 d -1 generik poin. Sementara jumlah kurva tersebut tidak tergantung pada pilihan poin, Mikhalkin melekat multiplicities positif untuk setiap kurva tropis sehingga jumlah tertimbang tidak, dan pada kenyataannya sama dengan N d . Dia juga berkurang multiplicities ini dan pencacahan kurva tropis dengan kombinatorika jalur kisi dalam segitiga panjang sisi d .
Mikhalkin digunakan korespondensi melibatkan peta Log :( C * ) 2 -> R 2 yang didefinisikan oleh ( x , y ) | -> (log | x |, log | y |), dan `batas kompleks besar tertentu ' struktur kompleks pada ( C * ) 2 . Di bawah batas kompleks besar ini, kurva rasional gelar d interpolasi 3 d -1 poin di ( C * ) 2 cacad untuk `kurva tropis kompleks ', yang gambar di bawah Log adalah kurva tropis biasa interpolasi gambar dari titik-titik. Banyaknya kurva tropis T adalah jumlah kurva tropis kompleks yang proyek untuk T .
Bagaimana kurva nyata? Berikut korespondensi ini, Mikhalkin melekat banyaknya nyata untuk setiap kurva tropis dan menunjukkan bahwa jika kurva tropis interpolasi diberikan 3 d -1 poin memiliki jumlah multiplisitas nyata N , maka ada 3 d -1 nyata poin yang disisipkan N nyata rasional kurva derajat d . Multiplisitas nyata ini lagi dinyatakan dalam jalur kisi.
Bagaimana invarian Welschinger ini? Dengan cara yang sama, Mikhalkin melekat berat ditandatangani untuk setiap kurva tropis (versi tropis tanda Welschinger) dan menunjukkan bahwa jumlah tertimbang yang sesuai sama Welschinger ini invarian. Seperti sebelumnya, berat badan menandatangani tropis ini dapat dinyatakan dalam jalur kisi.
Selama semester di MSRI, Itenberg, Kharlamov, dan Shustin [ IKS ] digunakan hasil Mikhalkin untuk memperkirakan Welschinger ini invarian. Mereka menunjukkan bahwa W d \ GEQ d ! / 3, dan juga
log W d = log N d + O ( d ), log N d = 3 d log d + O ( d ).
Jadi setidaknya logaritmik, sebagian kurva rasional gelar d interpolasi 3 d -1 nyata poin dalam pesawat adalah nyata.
Ada dua contoh lain dari fenomena ini batas bawah, yang pertama mendahului kerja Welschinger ini. Misalkan d bahkan dan membiarkan W ( s ) menjadi polinomial nyata derajat k ( d -k +1). Kemudian Eremenko dan Gabrielov [ EG ] menunjukkan bahwa terdapat polinomial nyata f 1 ( s ), ..., f k ( s ) gelar d yang determinan Wronski adalah W ( s ). Bahkan, mereka terbukti lebih rendah terikat pada jumlah k -tuples polinomial, hingga kesetaraan. Demikian pula, sementara pada MSRI, Soprunova dan saya [ SS ] mempelajari sistem polinomial jarang berhubungan dengan posets, menunjukkan bahwa jumlah solusi nyata dibatasi di bawah dengan tanda-ketidakseimbangan poset tersebut. Batas bawah seperti untuk masalah enumerative, yang menyiratkan adanya solusi nyata, yang penting untuk aplikasi.
Misalnya, cerita ini menceritakan lebih bir satu malam di Lokakarya MSRI pada Geometric Modeling dan Real aljabar Geometri pada bulan April 2004. Seorang peserta, Schicho, menyadari bahwa hasilnya W 3 = 8 untuk cubics menjelaskan mengapa metode dia dikembangkan selalu tampak bekerja. Ini adalah sebuah algoritma untuk menghitung parametrization perkiraan busur kurva, melalui nyata rasional kubik interpolasi 8 poin pada busur. Ini tetap untuk menemukan kondisi yang menjamin adanya solusi yang dekat dengan busur. Ini hanya diselesaikan dengan Fiedler-Le Touze, sebuah Postdoc MSRI yang pernah belajar cubics (tidak harus rasional) interpolasi 8 poin untuk membantu mengklasifikasikan kurva bidang nyata gelar 9.
Bibliografi
Kami berterima berterima kasih kepada editor kami, Silvio Levy dan anggota MSRI yang karyanya kami jelaskan.
